In the diagram above , EFGH is a circle, centre O, FH is a diameter and GE is a chord, which meets FH at right angle at point N. If NH is 8cm and EG= 24cm. Calculate FH

The chord ST of a chord ST of a circle is equal to the radius r of the circle. Find the length of the arc ST.

In the diagram above, XZ is the diameter of the circle XYZW with center O and radius $\tfrac{15}{2}cm$. If XY =12 cm, find the area of the triangle XYZ

 In the diagram above, O is the centre of the circle, POM is a diameter and $\angle MNQ={{42}^{\text{o}}}$. Calculate $\angle QMP$  

In the diagram above, PQR is a straight line and PS is a straight line and PS is a tangent to the circle QRS with $\left| PS \right|=\left| SR \right|$ and $\angle SPR={{40}^{o}}$.Find $\angle PSQ$

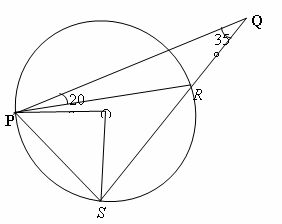
P, R and S lies on a circle centre O as shown above, while Q lies outside the circle. Find $\angle$PSO

In the diagram above, O is the centre of the circle $\angle UOT=70^\circ$ and $\angle RST=100^\circ$ Calculate $\angle RUO$

In the diagram POQ is a diameter of the circle. PQRS. If $\angle PSR={{145}^{o}}$. Find x^o           

Find the angle subtends at the centre of a circle by a chord which is equal in length to the radius of the circle.

From the diagram above, find x

An arc subtends an angle of 50^o at the centre of circle of radius 6cm. Calculate the area of sector formed

In the diagram above, PQR is a circle O. If $\angle \mathbf{QRP}$is x^o, Find $\angle \mathbf{QRP}$

$\begin{align}  & \text{Find the length of a chord which subtends an angle of 9}{{\text{0}}^{\text{o}}}\text{ at the centre of a } \\ & \text{circle whose radius is 8cm} \\ & \text{(A)  }4cm\text{  (B) }8cm\text{  }(C)\text{  }8\sqrt{2}cm\text{  (D) }8\sqrt{3}\text{ cm} \\\end{align}$

If the angle of a sector of a circle with radius 10.5cm is 120^o, find the perimeter of the sector

A chord of a circle of radius $\sqrt{6}cm$subtends an angle of 30^oon the circumference of circle. Find the length of the chord

From the diagram above, find the value of $\angle OTQ$

Calculate the perimeter of a sector of a circle of radius 12cm and angle 60^o

An arc subtends an angle of 30^oat the centre of a circle radius 12cm. Calculate the length of the arc

From the cyclic quadrilateral above, find $\angle TVS$